Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an = an.
Например, а=2, n=3: 2 * 2 * 2=2^3 = 8.
Вообще возведение в степень часто используется в различных формулах по математике и физике. Эта функция имеет более научное предназначение, чем четыре основные: Сложение, Вычитание, Умножение, Деление.
Возведение числа в степень
Возведение числа в степень – операция не сложная. Оно связано с умножением подобно связи умножения и сложения. Запись an – краткая запись n-ого количество чисел «а» умноженных друг на друга.
Рассмотри возведение в степень на самых простых примерах, переходя к сложным.
Например, 42. 42 = 4 * 4 = 16. Четыре в квадрате (во второй степени) равно шестнадцати. Если вам не понятно умножение 4 * 4, то читайте нашу стать об умножении.
Рассмотрим еще одни пример: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125. Пять в кубе (в третьей степени) равно ста двадцати пяти.
Еще один пример: 9^3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729. Девять в кубе равняется семи сотням двадцати девяти.

Формулы возведения в степень
Чтобы грамотно возводить в степень нужно помнить и знать формулы, указанные ниже. В этом нет ничего сверх естественного, главное понять суть и тогда они не только запомнятся, но и покажутся легкими.
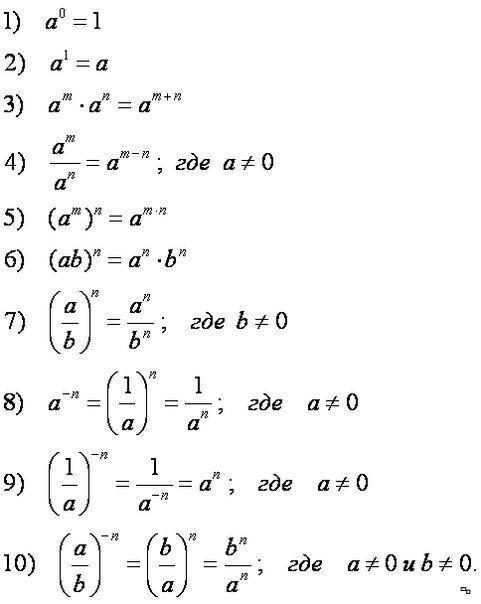
Возведение одночлена в степень
Что из себя представляет одночлен? Это произведение чисел и переменных в любом количестве. Например, двух – одночлен. И вот именно о возведении в степень таких одночленов данная статья.
Пользуясь формулами возведения в степень вычислить возведение одночлена в степень будет не трудно.
Например, (3x^2y^3)^2= 3^2 * x^2 * 2 * y^(3 * 2) = 9x^4y^6; Если возводить одночлен в степень, то в степень возводится каждая составная одночлена.
Возводя в степень переменную уже имеющую степень, то степени перемножаются. Например, (x^2)^3 = x^(2 * 3) = x^6;
Возведение в отрицательную степень
Отрицательная степень – обратное число. Что такое обратное число? Любому числу Х обратным будет 1/X. То есть Х-1=1/X. Это и есть суть отрицательной степени.
Рассмотрим пример (3Y)^-3:
(3Y)^-3 = 1/(27Y^3).
Почему так? Так как в степени имеется минус, то просто переносим в знаменатель данное выражение, а затем возводим в его в третью степень. Просто не так ли?
Возведение в дробную степень
Начнем рассмотрение вопрос на конкретном примере. 43/2. Что означает степень 3/2? 3 – числитель, означает возведение числа (в данном случае 4) в куб. Число 2 – знаменатель, это извлечение корня второй степени из числа (в данном случае 4).
Тогда получаем квадратный корень из 43 = 2^3 = 8. Ответ: 8.
Итак, знаменатель дробной степени может быть, как 3, так и 4 и до бесконечности любым числом и это число определяет степень квадратного корня, извлекаемого из заданного числа. Конечно же, знаменатель не может быть равным нулю.
Возведение корня в степень
Если корень возводится в степень, равной степени самого корня, то ответом будет подкоренное выражение. Например, (√х)2 = х. И так в любом случае равенства степени корня и степени возведения корня.
Если (√x)^4. То (√x)^4=x^2. Чтобы проверить решение переведем выражение в выражение с дробной степенью. Так как корень квадратный, то знаменатель равен 2. А если корень возводится в четвертую степень, то числитель 4. Получаем 4/2=2. Ответ: x = 2.
В любом случае лучший вариант просто перевести выражение в выражение с дробной степенью. Если не будет сокращаться дробь, значит такой ответ и будет, при условии, что корень из заданного числа не выделяется.
Возведение в степень комплексного числа
Что такое комплексное число? Комплексное число – выражение, имеющее формулу a + b * i; a, b – действительные числа. i – число, которое при возведение в квадрат дает число -1.
i^2=-1.
Рассмотрим пример. (2 + 3i)^2.
(2 + 3i)^2 = 22 +2 * 2 * 3i +(3i)^2 = 4+12i^-9=-5+12i.
Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Записаться на курсУзнать подробнее
Возведение в степень онлайн
С помощью нашего калькулятора, Вы сможете посчитать возведение числа в степень:
Загрузка калькулятора...
Возведение в степень 7 класс
Возведение в степень начинают проходить школьники только в седьмом классе.
Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an=an.
Например, а=2, n=3: 2 * 2 * 2 = 2^3 = 8.
Примеры для решения:

Возведение в степень презентация
Презентация по возведению в степень, рассчитанную на семиклассников. Презентация может разъяснить некоторые непонятные моменты, но, вероятно, таких моментов не будет благодаря нашей статье.
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше - записывайтесь на наш курс: Ускоряем устный счет - НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
